42.接雨水

力扣题目链接

题目内容

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

img

1
2
3
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

1
2
输入：height = [4,2,0,3,2,5]
输出：9

提示：

  • n == height.length
  • 1 <= n <= 2 * 104
  • 0 <= height[i] <= 105

解题思路

接雨水可以说是一道非常经典的面试题，最开始听说这道题是“某某面试官出了一道3d接雨水”，好奇搜了一下，确实被惊到了😲，感觉以自己这烂水平遇上了铁定是寄，因此对接雨水一直是"唯恐避之不及"，后来发现基础版本的接雨水其实难度也没那么大，做不到复杂度的极致，但努努力AC还是可以的。

当然由于本人水平较低，因此思路可能不是非常好，并且题解说的可能啰里吧嗦😭请读者选择性吸收。

1.分析问题

首先来看这道题的要求，是要求解给定的柱子排列能够接多少雨水，既然是要求能接多少雨水，那么我们肯定就需要考虑一个问题：什么因素会影响雨水的容量？

img2

以图中标注的雨水块为例，这部分雨水的容量为 1 * 1 = 1，那为什么是这个容量呢(小学生都知道，多此一举的问题:happy:)，🙌当然是因为木桶效应(也叫短板效应)！即一只水桶能装多少水取决于它最短的那块木板，因为桶中水的最大高度不能大于最短木板的长度。因此，对于图中标注的"桶"，它左边的木板为 1，右边的木板为 2，水的高度最高就是 1，因此容量就是(1 - 0) * 1。

知道了木桶效用，我们是可以求解出一个桶中所能接雨水的最大容量的。但显然这还不足以让我们求出这个问题，因为这里有很多的"木桶"，看起来我们是需要找到所有的"木桶"，并且求出他们的短板，再以此计算容量。这个时候就需要想办法将解决实际问题的思路转换成计算机程序能解决的方案了，我们需要找到一个规律，一个能让计算机理解的规律。

2.思考规律

再来看图，这次我们不再直接从图中找水(毕竟计算机并不能直接像图中这样清晰直观的找到水)，而是从第一个柱子开始依次往后遍历：

img2

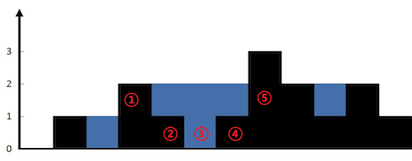
假设已经遍历到了如图中的 ① 处，以此处作为起点(假设我们已经知道它就是左短板了)，显然我们需要知道这个木桶右边的板子是哪个、有多高，这样我们就可以轻松求解出容量。

继续往后遍历到 ② ，② 的高度是比 ① 更矮，那么它可以作为木桶右边的木板吗？当然是可以的，任意两个木板都可以看做是一个桶，那么根据之前的思路，①和②所组成的桶，水的最大高度即为②的高度，容积即为 （height② - 0）* index② - index① = 0。

但这是我们想要的吗？显然从图中就可以看出并不是的，我们想要求的是**最大容积**，而如图中可见实际上除了 ① 和 ② 组成的桶(实际宽度为0的空桶)，① 还和 ⑤ 组成了更宽更高的桶，而这个大桶才是我们想要求解的那个。

那么我们该怎么找到这个最高的大桶呢？考虑木板 ①，他能组成的最高的桶，就是将它作为短板时组成的桶，即我们需要找到一个高度不小于 ① 的木板。

3.假设尝试

难点在于桶的组成有很多种可能，例如未必存在一个高度比 ① 高的，即便存在，也有很多的组桶方法。我们可以先从最简单的情况出发，想出一个大致的解题思路，再将其推及到更复杂的情况进行验证。

重新捋一下思路，我们想要求最大容量，就要求组成的水容量最高的桶，而已知一个左边界，它能组成的最高的桶，就是将它作为短板时组成的桶，即要找一个高度不小于①的板。

3.1存在更高的木板

img2

这里我们先做一个假设：木板 ① 的右边一定存在比它更高的木板，第一个比 ① 高的木板我们假设是 N (即图中的⑤)，而在 ① 和 N 之间则都是比 ① 和 N 更矮的木板，它们之间任意两个组合而成的木桶，显然高度都不会超过 ① 和 N 组成的这个大桶，即从 ① 到 N 这个区间，只有 ① 和 N 组成的桶是有意义的，因此我们只需要计算这个桶的容积，即 Σ①N-1 (h① - hi) * 1，显然这也是图中 ① 和 ⑤ 围起来的桶。

3.2右边界的选择

那么我们这种想法是对的吗？可以分析一下其他情况，考虑第一个问题：

为什么要找第一个比 ① 高的木板 N 呢？为什么不是和之后更高的木板来组成新的桶呢？

假设存在第 N + m 个木板，有 HN+m > H①， HN > H①：

​ | |

​ | | | |

​ | ① | | N | |N+m |

对于这三个木板，由于 HN > H①，因此 N 和 N + m 之间的水，只会受到 N 和 N+m 中的最小值的影响，而不会受到 ① 的影响，因此 ① 只能与 N 组成木桶，而不会与之后更高或更矮的木板组成木桶。即 N 由于比 ① 更高，因此阻挡了 ① 对于后面木桶的影响 (或者说N兜不住的水，① 也兜不住)。

结论：当我们确定了 ① 为左边界的时候，其对应的右边界一定是第一个比它高的板 N (如果存在的话)！

由此，我们也就可以确定下一个木桶的左边界，即为结论中所说 N，因为 N 左边的木板都比 N 矮，无法越过 N 影响右边的桶，这即前文中假设已知 ① 为左边界的原因。

这样问题又再次回到之前：知道左边界，如何求解它所组成的最高的桶？用第一个比左边界更高的板作为右边界！之后将该右边界作为新的左边界继续求解。

也就是说我们只需要重复计算上述该子问题即可，这也就变成了计算机程序能够理解的形式。

3.3不存在更高的木板

对于刚才的假设，显然它最大的反例就是：

当前 ① 作为左边界后，①已经是最高的木板了，它的右边不再有比它更高的木板了，这个时候该怎么办呢？

其实到了这个时候，木板 ① 左边的水已经全部求解完了(若①为第一个左边界，水即为0)，而我们在求解这部分水的时候，思路就是前面的子问题求解：用第一个比左边界更高的板作为右边界组成桶。

那么同理我们求 ① 右边的部分，只需要将思路反过来即可：要使 ① 组成最高的桶，而 ① 又不可能作为短板，即求剩余板中最高的板 M ，这样组成的桶才是最高的，因为 M 会阻断右边更矮的木板对 ①-M 桶的影响！

同理将 M 再作为新的左边界，继续重复该子问题，即可求出最终答案。

当然这个思路显然是有些麻烦的，例如对于右边最高板的寻找，因为我们之前是在线性遍历，最高值就不太容易求解。其实这个时候如果画个图，就会很清晰直观的想到一个新的思路：

img2

还是这张图，根据刚才的思路，我们会从左到右一直算到 ⑤，之后就没有比它更高的了。而 ⑤ 有个很明显的特征：这个 ⑤ 一定是所有木板中最高的那个！

即我们从左边开始遍历所有的木板，到达最高点就会停下，那如果我们从右边开始向左遍历呢？即将这些木板镜像反转一下，显然还是会到达最高点 ⑤ 后停下，所以说我们只需要再用完全相同的计算逻辑反过来遍历即可求解出剩下的桶中的水！

4.代码实现

对上述内容进行总结，得到问题求解思路：

**首先从左往右遍历木板，以第一个木板为左边界，寻找第一个比它高的木板(或相等，即不低于)，作为右边界，求解这两个木板组成的桶内水的容量。**即我们需要两个变量来分别记录左边界的位置和当前遍历的位置，再加上记录结果值，即可得到如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int res = 0;

int left = 0; 	// 左边界的位置
int index = 0;  // 遍历木板 找到当前左边界对应的右边界
while (++index < height.size()) {
    if(height[index] >= height[left]) {
        // 找到第一个比当前左边界高的木板(即右边界)！
        // 计算这个桶内的水:
        int minh = height[left]; //当前木桶短板(即水高度)
        for(; left < index; left++) { // 将水累加
            res += minh - height[left];
        }
    }
}

**之后我们再以完全相同的思路从右往左遍历木板，以第一个木板为右边界，寻找第一个比它高的木板(或相等，即不低于)，作为左边界，求解这两个木板组成的桶内水的容量。**当然此时我们的终止条件就不需要是 index >= 0了，index 只需遍历到最高点，也就是现在的 left 即可，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
int right = height.size()-1; // 右边界的位置
index = height.size()-1; 	 // 遍历木板找到当前右边界对应的左边界
while (--index >= left) {
    if(height[index] >= height[right]) {
        // 找到第一个比当前右边界高的木板(即左边界)！
        // 计算这个桶内的水:
        int minh = height[right]; //当前木桶的短板
        for(; right > index; right--){
            res += minh - height[right];
        }
    }
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int trap(vector<int>& height) {
        int res = 0;

        int left = 0; 	// 左边界的位置
        int index = 0;  // 遍历木板找到当前左边界对应的右边界
        while (++index < height.size()) {
            if(height[index] >= height[left]) {
                // 找到第一个比当前左边界高的木板！
                int minh = height[left++]; //当前木桶的短板
                for(; left < index; left++) {
                    res += minh - height[left];
                }
            }
        }

		// 求完最高点的左边部分 开始从右往左遍历
        int right = height.size()-1; // 右边界的位置
        index = height.size()-1; 	 // 遍历木板找到当前右边界对应的左边界
        while (--index >= left) {
            if(height[index] >= height[right]) {
                // 找到第一个比当前右边界高的木板！
                int minh = height[right]; //当前木桶的短板
                for(; right > index; right--){
                    res += minh - height[right];
                }
            }
        }
        return res;
    }
};
#Leetcode
42.接雨水
https://mmma.top/2023/07/06/接雨水问题/
作者
MMMa
发布于
2023年7月6日
许可协议